Adaptive Hybrid Reduced Differential Transform Method in Solving Nonlinear Schrodinger Equations

Abstract

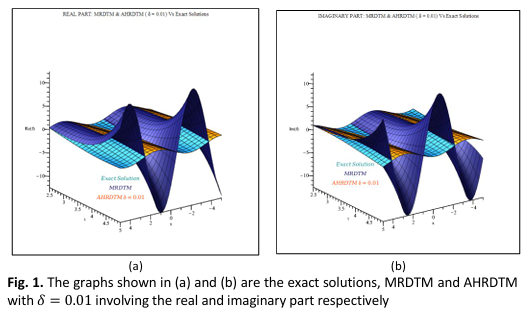
In this paper, piecewise-analytical and numerical solutions are obtained by a new adapted approach named the Adaptive Hybrid Reduced Differential Transform Method (AHRDTM). The fundamentals of the method are introduced, followed by its application to Nonlinear Schrodinger Equations (NLSEs). Analytical and numerical solutions are acquired using piecewise convergent series with computationally feasible components across a sequence of sub-intervals of varying length. This succeeds due to the adaptive algorithm introduced and the substitution of the non-linear term in the NLSEs with their corresponding Adomian polynomials. The accuracy of the AHRDTM is observed through numerical comparisons between the proposed method and the Modified Reduced Differential Transform Method (MRDTM) with their respective exact solutions. The absolute errors presented in the table reveal that the proposed approach has better accuracy in solving the considered equations. The results and pictorial illustrations have been provided to demonstrate the reliability of the method’s accuracy in obtaining approximate solutions.