Solution of the Porous Medium Equation with Source Terms via 4-Point Newton-Explicit Group MKSOR Based on Wave Variable Transformation

Abstract

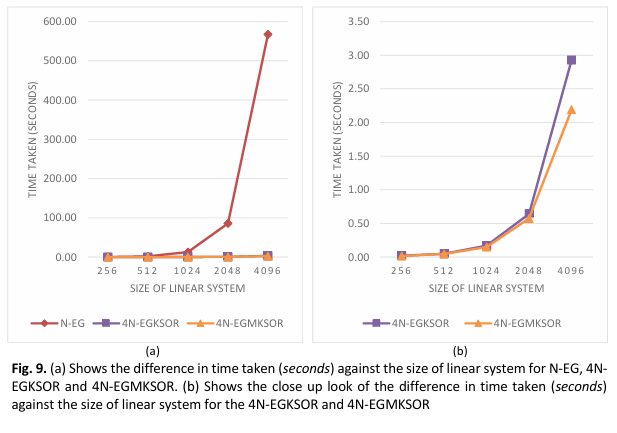
This paper presented the 4-point Newton-Explicit Group Modified Kaudd-SOR (4N-EGMKSOR) iterative method combined with the wave variable transformation to solve the porous medium equation with source terms (PMES). The PMES is a nonlinear heat equation having a variety of naturally occurring physical applications, primarily describing processes involving fluid flow, heat transfer and diffusion. However, finding its exact solution can be difficult. Hence, a numerical method is a good option to obtain the approximate solution for the proposed problem. Firstly, we applied the wave variable transformation to the PMES to reduce the PMES into an ordinary differential equation (ODE). This reduction will significantly minimize the computational complexity of the approximate solution for the PMES. Furthermore, the finite difference scheme was used to discretize the reduced form of the PMES, which leads to a nonlinear finite difference approximation equation. The approximate nonlinear equation was then solved using the Newton method, yielding a system of linear equations. In order to solve the formed system of linear equations, the 4N-EGMKSOR was developed and its formulation was derived. In addition, the effectiveness of the proposed method was examined by performing some numerical calculations and the results were compared to the existing iterative methods, i.e., the Newton-Gauss Seidel (N-GS) and the 4-Point Newton- Explicit Group Modified Kaudd SOR (4N-EGMKSOR). Based on the comparison, the 4N-EGMKSOR iterative method proposed in this work is more efficient in getting the converged solution of the PMES compared to N-GS and 4N-EGKSOR iterative methods.